— 190 —
dat het als een plat vlak kan beschouwd worden, zoo als A B in figuur 2,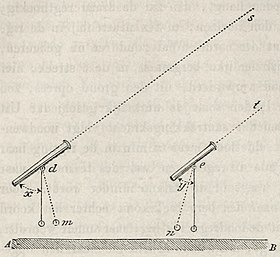 
dan zijn de rigtingen van het schietlood in d en e beiden loodregt op dit vlak en derhalve onderling evenwijdig. Nemen wij aan, dat in de punten d en e twee verrekijkers zijn geplaatst en beiden gerigt op eene en dezelfde vaste ster, dan zal wegens den verbazende afstand der vaste ster, ook de as van den eenen verrekijker evenwijdig moeten zijn met de as van den anderen kijker, of de lijn d's evenwijdig aan e t. Hieruit volgt nu, dat het schietlood in de beide plaatsen met de verrekijkers twee hoeken x en y vormt, die onderling gelijk zijn. Deze gelijkheid heeft echter niet meer plaats, indien de oppervlakte A B te groot is, om nog als een plat vlak te kunnen worden aangezien. Het verschil dat bestaat, laat zich intusschen uit den afstand d e en den straal des aardbols gemakkelijk berekenen.
Nemen wij thans het eenvoudigste geval aan, dat is, dat de hoeken x y gelijk zijn, en verbeelden wij ons vervolgens, dat er tusschen de beide kijkers in d en e de berg c der figuur 1 geplaatst wordt. Het schietlood in d verkrijgt dan de rigting d m en dat in e de rigting e n. Men zal aanstonds zien, dat dan de hoek x grooter en de hoek y kleiner moet worden. Bevindt zich bovendien de berg juist in het midden van d en e, dan zullen ook de beide afwijkingen van de loodlijnen gelijk zijn, en deze afwijking zal klaarblijkelijk gelijk zijn aan het halve verschil der beide hoeken, die nu door de draden der schietlooden met de as van de verrekijkers gevormd worden.
Dit is de manier, om na te gaan, of er eene afwijking van het schietlood in de nabijheid van enkele bergtoppen bestaat en hoe-
