Album der Natuur/1854/Baan van de aarde om de zon, Reitsma
| Over de baan die de aarde rondom de zon beschrijft (1854) door Anne Tjittes Reitsma |
| Over de baan die de aarde rondom de zon beschrijft werd gepubliceerd in Album der Natuur (derde jaargang (1854), p. 33–60. Dit werk is in het publieke domein. |
Als wij eenen blik slaan op de onmetelijke ruimte des heelals, dan doen zich daar afstanden en grootheden aan ons voor, waarbij de koenste verbeeldingskracht duizelt. Dan wordt de aarde, die wij bewonen, een naauwelijks merkbaar stipje, dat in die oneindige ruimte in het niet verzinkt,—één droppel in dien oceaan van werelden, die over het grenzenloos gebied der schepping zijn uitgestrooid, een zonnestofje, een zandkorrel, wiens bestaan zelfs niet vermoed zal worden op eene van die wereldbollen en sterrenstelsels, die wij in de diepte van het hemelruim met teleskopische blikken bespieden.
En toch is er geen plekje in de scheppingsruimte, hetwelk ons nader ligt en grooter belangstelling inboezemt, dan de aarde, die wij bewonen, die wij liefhebben, waarop wij geboren worden, leven en sterven, waar wij onze ontwikkeling aanvangen om ze misschien op andere wereldbollen te voltooijen. En welk een uitgebreid veld opent zich hier niet voor onze zucht naar kennis en wetenschap! Wij kunnen de natuurlijke gesteldheid van haar ligchaam tot het onderwerp onzer navorschingen stellen. Dit is de taak der physische aardbeschrijving. Wij kunnen het wonderbare zamenstel van hare oppervlakte ontleden, of afdalen in de diepte, om in de op elkander volgende lagen en formatiën het geheim harer wording na te sporen. Maar wij kunnen haar ook beschouwen in hare verhouding tot het zonnestelsel, waarvan zij een deel uitmaakt. Wij kunnen den [ 34 ]schakel, waardoor zij zamenhangt met dat stelsel van werelden, waarin de zon met de van haar afhankelijke ligchamen eene plaats bekleedt, de wetten, aan welke zij gehoorzaamt, de verschijnsels, die zij aanbiedt, de plaats, die zij als individueel lid in dat wereldstelsel inneemt, trachten na te vorschen. Dit is de taak der astronomische aardbeschrijving.
Wij hebben ons voorgenomen één enkel punt uit de veelomvattende wetenschap der astronomische aardbeschrijving voor onze lezers in het licht te stellen, en de baan, die de aarde rondom de zon beschrijft, hen nader te doen kennen.
Er wordt hier dus als bewezen voorondersteld, dat de aarde eene baan rondom de zon beschrijft, dat zij zich dus rondom de zon, en niet de zon zich rondom de aarde beweegt. Die vooronderstelling is voorwaar geene kleinigheid. Het mag voor eene der schoonste overwinningen op het gebied der sterrekunde gehouden worden, dat een copernicus, in weerwil van de schijnbare beweging der zon rondom de aarde, het onwederlegbare bewijs leverde, dat dit slechts een bedriegelijke schijn is, en dat daarentegen de aarde zich werkelijk rondom de zon beweegt. Het mag voor een treffend bewijs van het erkende gezag der sterrekundige wetenschap gelden, dat men deze stelling, die eens voor eene groote ketterij gehouden werd, althans voor het beschaafde publiek als eene erkende waarheid mag aannemen. De zinnelijke waarneming toch maakt op ons geenen anderen indruk, dan dat de aarde onbewegelijk vast staat, en dat de zon en alle hemelligchamen zich rondom haar bewegen. En desniettegenstaande vindt de wetenschap geloof zelfs bij hen, die hare bewijsvoeringen niet kunnen volgen, en op haar gezag wordt als waarheid aangenomen, wat tegen de eigene zinnelijke waarneming indruischt, namelijk dat de aarde rondom de zon haren loop volbrengt.
Mag men dit nu als eene waarheid aannemen, die voor allen, die in de kennis der natuur belang stellen, geen opzettelijk bewijs noodig heeft, er blijven dan toch vele vragen te beantwoorden, vele ophelderingen te geven aangaande den weg, dien de aarde doorloopt en dien wij met haar, door haar gevoerd en gedragen, door [ 35 ]de onmetelijke ruimte afleggen. De aarde toch is het voertuig, de ontzaggelijke ballon, waarop wij met millioenen togtgenooten zonder het te merken met eene verbazende snelheid eene groote, zeer groote reis door het onbegrensde rijk der schepping volbrengen. Zouden wij het dan niet van belang achten de baan, die de aarde doorloopt, en den weg, dien wij met haar afleggen, eenigzins nader te leeren kennen?
Wij zullen daarom de voornaamste eigenschappen van die baan nader trachten te verklaren, en daartoe onze aandacht bepalen:
- vooreerst, bij de gedaante van die baan,
- ten tweede, bij hare grootte,
- ten derde, bij de stelling der aarde op die baan,
- ten vierde, bij de beweging der aarde in die baan,
- ten vijfde, bij de verplaatsing van die baan in de ruimte.
I.
OVER DE GEDAANTE VAN DE BAAN, DIE DE AARDE RONDOM DE ZON BESCHRIJFT.
Er was ongetwijfeld eene groote schrede voorwaarts gedaan, toen
copernicus het bewijs had geleverd, dat de aarde zich rondom de zon beweegt. Het was zeer natuurlijk, dat men zich de baan, die de aarde rondom de zon beschrijft, als eenen cirkel voorstelde. Maar indien de baan der aarde eenen volmaakten cirkelvorm hadde, dan moest ook de afstand der aarde van de zon in elk punt van hare loopbaan dezelfde zijn, omdat elk punt in den omtrek van eenen cirkel even ver van het middelpunt is verwijderd; maar dan moest ook de snelheid, waarmede de aarde in hare baan voortgaat, altijd dezelfde zijn, omdat bij gelijken afstand van de zon ook de oorzaak, die de aarde voortbeweegt, met gelijke kracht op haar moest werken. Maar nu bemerkte men al spoedig bij voortgezette waarneming, dat dit werkelijk niet het geval is, dat de afstand der aarde van de zon niet altijd gelijk en de snelheid harer beweging [ 36 ]niet altijd dezelfde is. Het was vooral de met onvermoeide volharding voortgezette waarneming van dit verschijnsel, die den grooten kepler tot de ontdekking leidde van de ware wetten, waardoor het gansche zonnestelsel wordt beheerscht, en die later in de door newton ontdekte wet der algemeene zwaarte hare volkomene verklaring en bevestiging vonden. Het resultaat van keplers waarnemingen was, dat de beweging der planeten en dus ook der Aarde plaats heeft, niet in een' cirkel, maar in eene ellips.
Wat is eene ellips? Om zich daarvan een duidelijk denkbeeld te maken, heeft men slechts te letten op de wijze, waarop men zulk eene ellips zeer gemakkelijk kan teekenen. Als men in twee punten op een effen vlak twee nagels of pennen vastzet, dan een koord, waarvan de einden aan elkander zijn geknoopt, om die pennen legt en dan met een tusschen de koord gehouden potlood die koord stijf uitspant; als men vervolgens dat potlood op de effene vlakte laat rondgaan, terwijl men zorgt, dat de koord steeds goed gespannen blijft, dan verkrijgt men een langwerpig rond of ellips. De twee punten, om welke de koord loopt, heeten de brandpunten, terwijl het punt, hetwelk juist in het midden tusschen de brandpunten ligt, het middelpunt van de ellips genoemd wordt. Hoe nader de brandpunten aan elkander geplaatst zijn, des te meer nadert de ellips tot de cirkelvormige gedaante; hoe verder de brandpunten van elkander zijn verwijderd, des te langwerpiger wordt de ellips. Als men nu door de twee brandpunten eene regte lijn trekt, die aan beide zijden den omtrek der ellips raakt, dan noemt men die lijn de lange as van de ellips. Wanneer men door het middelpunt eene loodlijn trekt, die aan beide zijden tot den omtrek wordt voortgezet, noemt men die de korte as van de ellips. Den afstand tusschen een der brandpunten en het middelpunt, noemt men de excentriciteit of uitmiddelpuntigheid. De regte lijnen, die uit een der brandpunten naar den omtrek worden getrokken, noemt men de voerstralen der ellips.
Op de nevensgaande figuur zijn d en e de brandpunten, c het middelpunt, a b de groote as, f g de kleine as, c e of c d de uitmiddelpuntigheid, en e k, e i, e h voerstralen. De beide voerstralen [ 37 ]d f en e f stellen de koord voor, door welker rondbeweging om de brandpunten d en e de omtrek der ellips geteekend is.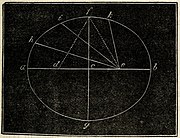
Fig. 1.
Doch nu ontstaat de vraag: wat mag toch wel de oorzaak zijn, dat [ 38 ]de aarde zich niet in eenen cirkel, maar in eene ellips rondom de zon beweegt? Men zoude anders denken, dat de aantrekkingskracht, die de zon op haar uitoefent, omdat ze altijd even sterk is, haar ook altijd op gelijken afstand moest houden, en dat zij bij gevolg eenen volmaakten cirkel om de zon beschrijven moest.
Om ons dit nog al ingewikkeld vraagstuk te verklaren, moeten wij letten op een verschijnsel, hetwelk onder ieders waarneming valt. Indien twee verschillende krachten in denzelfden tijd in verschillende rigtingen op een ligchaam inwerken, zal dat ligchaam niet de rigting van de eene of de andere kracht volgen, maar in eene tusschen die beide inliggende rigting worden voortgestooten; het zal, gelijk men het in de mathematische kunsttaal noemt, in gaan in de diagonaal van den parallelogram.
Als op een ligchaam (zie fig. 2,3,4) in a geplaatst, op hetzelfde
Deze algemeene wet is hier ten volle toepasselijk. Het is geene enkele kracht, maar het zijn twee krachten, in vermogen en rigting zeer verschillende, die de beweging der aarde om de zon bepalen. De eerste kracht is de aantrekking, welke het ligchaam der zon op de aarde uitoefent. Indien deze kracht alleen op de aarde inwerkte, dan zoude de aarde steeds in eene regte lijn en met toenemende snelheid tot de zon naderen, totdat zij eindelijk geheel op de zon nederviel. Deze kracht werkt dus in eene rigting, die naar het centrum of middelpunt der zon gekeerd is, en wordt daarom ook de centraalkracht genoemd. De andere kracht is die impulsie, die stoot, waardoor aan iedere planeet bij hare wording eene eigene, oorspronkelijke beweging is medegedeeld. Door deze kracht wordt dus de aarde aangedreven om in de eenmaal gegevene rigting desgelijks in eene regte lijn voort te gaan. Indien deze kracht de eenige ware, die op haar inwerkte, dan zoude zij sedert hare wording onafgebroken in die rigting zijn voortgegaan en zich steeds verder van de zon verwijderd hebben. Men noemt ze, omdat ze in den tangens of raaklijn van hare baan gerigt is, de tangentiaal- ook wel de centrifugaal of middelpuntschuwende kracht. De zamenwerking van deze twee krachten bepaalt de beweging der aarde.
Stellen wij, dat in fig. 5 c de zon en a de aarde aanwijst.
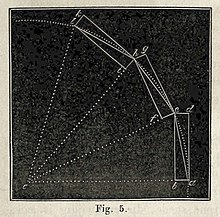Indien nu de kracht, waarmede de zon het ligchaam der aarde in de rigting a c aantrekt, het vermogen heeft om in een gegeven tijd de aarde uit a naar b te verplaatsen, terwijl de aarde door de haar gegevene impulsie, dat is door de tangentiaalkracht, in dienzelfden tijd van a tot d zoude voortgaan, dan zal zij, volgens de boven verklaarde wet, in den gegeven tijd door den diagonaal [ 40 ]des parallellelograms gaan, en dus in e zijn aangekomen. Indien zij nu in e aangekomen wederom denzelfden stoot krijgt, door de zamenwerking van de centraal- en tangentiaalkracht, zal zij in even grooten tijd in h gekomen zijn en zoo wederom in l enz. Zij zoude dus een veelhoek a e, e h, h l enz. beschrijven, tot dat ze eindelijk wederom in a zou zijn teruggekeerd.
Daar nu echter de beide krachten, die de beweging der aarde bepalen, niet bij regelmatig terugkeerende stooten haar vermogen oefenen, maar onafgebroken en in elk punt des tijds gelijkelijk doorwerken, zoo wordt daardoor bewerkt, dat de baan, die de aarde beschrijft, niet uit eene menigte regte lijnen zamengesteld, geen veelhoek zijn kan, zoo als op fig. 5 is voortgesteld, maar dat zij eene voortloopende kromme lijn zijn moet, die over de punten a, e, h, l loopt en eindelijk tot a terugkeert. Maar nu leert de wiskunde, dat in dit geval deze kromme lijn noodzakelijk den vorm van eene der zoogenaamde kegelsneden moet aannemen.
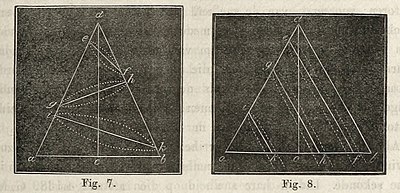
Als wij eenen regthoekigen driehoek om eene van de zijden, die den regthoek vormen, omdraaijen, dan beschrijven wij een ligchaam, welks grondvlakte een cirkel is en welks gebogene oppervlakte in eene spits uitloopt. Zulk een ligchaam noemt men eenen kegel. Nu kan men dat ligchaam door eene platte doorsnede in verschillende rigtingen doorsnijden.
Snijdt men den kegel zoo door, als in fig. 6, dat de doorsneden evenwijdig zijn aan de grondvlakte, dan verkrijgt men vlakten, die volkomene cirkels zijn, zoo als bij de aan de grondvlakte a b evenwijdige doorsneden e f, g h, i k het geval is.—Snijdt men den kegel met eene doorsnede, die niet aan de grondvlakte evenwijdig is, maar toch door de as d c des kegels gaat lig. 6. en dus den gebogenen omtrek geheel doorsnijdt, zoo als in fig. 7 bij de doorsneden e f, g h, en i k het geval is, dan noemt men die doorsneden ellipsen.—Doch men kan den kegel ook doorsnijden met eene snede, die evenwijdig is aan [ 41 ]de schuinsche zijde van den kegel.
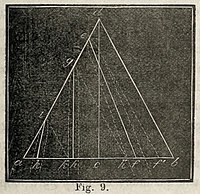Deze kromme lijnen nu dragen den naam van hyperbolen.
Daar de beweging der aarde, gelijk wij boven hebben aangetoond, door de zamenwerking van twee verschillende krachten, de centraal- en tangentiaalkracht, bepaald wordt, zoo volgt daaruit reeds op wiskundige gronden, dat zij, even als elk ander planetenligchaam, zich van hare wording af in eene van die kromme lijnen moet bewegen: dat zij dus òf eenen cirkel, òf eene ellips òf eene parabool, òf eene hyperbool moet beschrijven. Elke andere gedaante van hare baan wordt op wiskundige gronden als onmogelijk erkend.
[ 42 ]Nu is de vraag, in welke van deze kromme lijnen een planetenligchaam zich zal voortbewegen. Dit hangt af van twee factoren: vooreerst, van de snelheid der beweging, welke aan een ligchaam bij zijne wording is medegedeeld, en ten tweede, van den afstand, waarop een ligchaam van de zon geplaatst is, omdat daardoor de aantrekkingskracht, die de zon daarop uitoefent, wordt bepaald. De wiskunde geeft ons de vaste wetten aan de hand, volgens welke wij kunnen berekenen, welke uitwerking deze beide factoren met opzigt tot de banen der planeten moeten hebben.
Als onze aarde zich in haar perihelium, dus het naast bij de zon bevindt, gaat zij voort met eene snelheid van 4,1846 Geog. Mijlen in eene sekonde. Indien hare snelheid op dien afstand 4,1389 G. M. bedroeg, dan zoude zij eenen volkomenen cirkel rondom de zon beschrijven. Ware de snelheid harer beweging minder, dan zoude zij in eene ellips rondgaan, wier middellijn korter zoude zijn dan de middellijn van dien cirkel. Nu echter hare werkelijke snelheid het bedrag van 4,1389 te boven gaat, moet zij eene ellips beschrijven, wier middellijn die van dien cirkel te boven gaat. Had zij op dat punt eene snelheid van 5,8532 G. M., dan zoude hare loopbaan eene parabool uitmaken. Bij eene nog grootere snelheid zoude zij eene hyperbool beschrijven. In de twee laatste gevallen zoude de aarde niet meer tot het planetenstelsel behooren, daar zij, de rigting van den eenen tak des parabools of des hyperbools tot in het oneindige volgende, steeds verder in de diepten der oneindige ruimte zoude voortgaan, zonder ooit tot de zon terug te keeren. Maar nu hare oorspronkelijke snelheid meer is dan 4,1389 G. M. en minder dan 5,8532 G.M. in eene sekonde, nu moet hare loopbaan noodwendig eene elliptische zijn.
Het spreekt van zelf, dat dit bedrag der snelheid bij de verschillende planeten geëvenredigd is aan hare afstanden van de zon. Jupiter, bij voorbeeld, de grootste planeet van ons zonnestelsel, zoude zich in eenen volkomenen cirkel bewegen, indien hare oorspronkelijke snelheid bij haren kortsten afstand van de zon, 1,8443 G. M. in eene sekonde bedroeg. Indien zij op dat punt eene snelheid van 2,6082 G. M. bereikte, zoude zij in eene parabool, bij nog [ 43 ]grootere snelheid in eene hyperbool voortgaan, dat is in beide gevallen eene oneindig groote loopbaan beschrijven. Maar nu hare wezenlijke snelheid op dat punt 1,8941 G. M. in de sekonde bedraagt, nu wordt zij juist door die snelheid in betrekking tot haren afstand van de zon genoodzaakt eene ellips te beschrijven.
Uit dit alles volgt derhalve op wiskundige gronden, dat de gedaante van de baan der aarde rondom de zon noodzakelijk eene elliptische zijn moet.
II.
OVER DE GROOTTE VAN DE BAAN, DIE DE AARDE RONDOM DE ZON BESCHRIJFT.
Om de eigenschappen van eene elliptische loopbaan des te beter in het oog te doen vallen, hebben wij in fig. 1 eene ellips van aanmerkelijke excentriciteit geteekend. Wij moeten ons echter niet voorstellen, dat de baan der aarde eene zoo langwerpige ellips vormt. Uit hetgeen wij over de gedaante dier baan gezegd hebben, valt gemakkelijk af te leiden, dat zij slechts weinig van eenen volkomen cirkel kan verschillen.
Wij hebben gezien, dat de oorspronkelijke snelheid, waarmede de aarde in hare baan voortgaat, slechts 0,0457 G. M. in de sekonde verschilt van die snelheid, die haar zoude noodzaken eenen volkomen cirkel te beschrijven. Uit dit gering verschil in snelheid volgt, dat ook de afwijking van den cirkelvorm slechts zeer gering kan zijn, en dat bij gevolg de ellips, die zij beschrijft, geene groote excentriciteit kan bezitten.
Wij zien dit bevestigd, als wij opmerken, dat de verste en naaste afstand, waarop de aarde op de tegenovergestelde punten van hare baan van de zon geplaatst is, niet eens zoo aanmerkelijk verschillen, dat wij dat verschil met ons oog uit de toe- of afneming der grootte van de zonneschijf kunnen waarnemen. Was dat verschil waarlijk in het oog loopend groot, dan zoude de zonneschijf zich in onze grootste nabijheid van dat ligchaam grooter en [ 44 ]op den versten afstand veel kleiner voordoen. Nu is dat verschil zoo gering, dat het niet dan door zeer naauwkeurige metingen kan worden waargenomen. Het is ons een nieuw bewijs, dat die afstanden niet veel verschillen, met andere woorden, dat de ellips, die onze aarde beschrijft, slechts weinig van den cirkelvorm afwijkt.
Om nu de ware grootte van de elliptische baan der aarde te kennen, behoeft men slechts aan de beide uiteinden van de groote as der loopbaan, den afstand van de zon, die in een der brandpunten staat, naauwkeurig te meten. Als de aarde (zie fig. 1) in haar perihelium b is, en men daar den afstand van de zon e b meet, en dan later als de aarde in haar aphelium, in a, is, weder den afstand van de zon a e meet; als men dan die twee afstanden zamentrekt, heeft men de geheele lengte van de lange as der baan a b. Als men dan weder van de helft van die lange as, c b, den kortsten afstand van de zon e b aftrekt, dan verkrijgt men daardoor c e als het bedrag der excentriciteit. Is dit eenmaal door waarneming bekend, dan is de geheele ellips in alle hare afmetingen ligt te berekenen.
Uit die waarnemingen is volgens de laatste zeer naauwkeurige bepaling van encke gebleken, dat de naaste afstand van de aarde tot de zon bedraagt 20,335,073 G. M., de verste afstand 21,029,585, hetwelk een gemiddelden afstand geeft van 20,682,329 G. M. De geheele lengte van de halve groote as der aardbaan bedraagt dus de ontzaggelijke som van 41,364,658 G. M. Het bedrag der excentriciteit is gevolgelijk ongeveer 17⁄1000 of naauwkeuriger in decimalen uitgedrukt, 0,016792 van de halve groote as; dat is eene lengte van 347256 G. M.
Alhoewel eene lengte van 347 256 G. M. nog al aanzienlijk genoemd mag worden, zoo is zij toch niet te vergelijken met de verbazende uitgebreidheid van de geheele baan der aarde. Om ons daarvan eene zinnelijke voorstelling te geven, behoeven wij slechts de verschillende grootheden, tot de baan der aarde betrekkelijk, met elkander te vergelijken.
Onze aarde heeft op hare evenachtslijn eenen omtrek van omstreeks 5400 G.M. en eene middellijn van 1719 G.M. of, naauwkeuriger [ 45 ]uitgedrukt, van ongeveer 12,754,980 Ned. ellen. Indien wij nu eene afbeelding van de baan der aarde wilden maken, en in die afbeelding aan de middellijn der aarde slechts de geringe lengte van 1⁄10 streep (0,0001 N. el) gaven, dan zoude het ligchaam der zon naar diezelfde evenredigheid eene middellijn van twaalf streep (0,012 N. el) moeten hebben, omdat haar middellijn ongeveer gelijk staat aan 120 middellijnen van onzen aardbol, met andere woorden, omdat 120 bollen, als onze aarde, naast elkander op de middellijn der zon geplaatst zouden kunnen worden. Dat ontzaggelijke hemelligchaam, hetwelk in inhoud onze aarde l½ millioen malen te boven gaat, zoude dus worden voorgesteld door een' bol van 12 Ned. streep in de middellijn. Maar de geheele groote as van de baan der aarde zoude, daar zij meer dan 24,000 maal de middellijn der aarde bevat, naar diezelfde evenredigheid eene lengte moeten beslaan van ongeveer twee el en vier palmen (2,4 Ned. el). Daar echter het bedrag der excentriciteit ongeveer 200 maal de middellijn der aarde overtreft, zoo zoude men het brandpunt, waarin de zon staat, op die middellijn van 2,4 Ned. el slechts 2 duim van het middelpunt af behooren te plaatsen. En wanneer men nu op die middellijn volgens de aangegevene afmetingen eene ellips beschrijft, dan moet het al een zeer scherp en geoefend gezigt zijn, hetwelk ze met het bloote oog van eenen cirkel zal kunnen onderscheiden. Hieruit volgt van zelve, dat men bij eene afbeelding op kleine schaal de elliptische gedaante der baan in het geheel niet kan uitdrukken en ze eenvoudig als eenen cirkel met de zon in het middelpunt beschrijft.
Ware de baan der aarde een cirkel, zij zoude een omtrek van bijna 130 millioen G.M. bezitten; nu zij eene ellips is, is de omtrek kleiner en bedraagt ongeveer 115 millioen G.M. Honderd vijftien millioen G.M.! Dat is dan de verbazende ruimte, die onze aarde jaar op jaar van hare wording af heeft doorloopen, dat is de weg, dien wij jaarlijks met haar door het onbegrensde gebied der schepping afleggen.
Om ons van zulke ontzaggelijke afstanden en van de snelheid, waarmede zij doorkliefd worden, eenige voorstelling te vormen, [ 46 ]doen wij best ze te vergelijken met andere ons bekende snelheden. Een snelzeilend schip legt in één uur een weg van ongeveer 3½ G.M. af. Een stoomwagen doorloopt in dien tijd 6 tot 8 G.M. Het geluid doorklieft in één uur tijds eene ruimte van 163 G.M. Een vier-en-twintig ponder, zoo hij onafgebroken met dezelfde snelheid, waarmede hij het kanon verlaat, kon voortgaan, zoude 250 mijlen afleggen. Maar dat alles is slakkengang bij de snelheid, waarmede onze aarde op hare baan voortijlt. Zij doorvliegt bij gemiddelde snelheid in één uur tijds eene ruimte van bijna 15,000 G.M.
III.
OVER DE STELLING DER AARDE OP HARE BAAN.
Om ons eene juiste voorstelling te vormen van den weg, dien de aarde aflegt, is het niet genoeg de gedaante en grootte der baan te kennen, maar moeten wij ook weten, hoe zij in hare baan geplaatst is. Als wij eene aardglobe voor ons zetten, en ons verbeelden, dat de rand der globe, tot in het oneindige verlengd, de vlakte is, waarin de aarde zich voortbeweegt, dan valt het in het oog, dat de aarde in die vlakte zeer verschillende standen kan aannemen, met andere woorden, dat de hoek, dien de aequator der aarde met de vlakte der ecliptica, dat is met die der aardbaan, maakt, zeer ongelijk kan zijn.
Naauwkeurige waarnemingen hebben geleerd, dat deze hoek, welken men de schuinscheid der ecliptica noemt, omstreeks 23½° bedraagt, of, volgens de opgave van peters voor het jaar 1850, 23° 27' 30" 76. Bijgevolg is de hoek, dien de as der aarde met de vlakte van de loopbaan vormt, ongeveer van 66½°.
Gesteld dat in fig. 10, g h de vlakte der ecliptica is, en a b de aequator, dan zal de hoek door die beide gemaakt, g c a of b c h = 23½° de schuinschheid der ecliptica bepalen en de as, die door de polen d e gaat, den stand der aarde op hare baan aanwijzen.
Men denke niet, dat de stelling der aarde op hare baan eene onverschillige zaak is. Juist aan dien schuinschen stand onzer planeet hebben wij de geregelde toe- en afneming van dag en [ 47 ]nacht, van licht en warmte, en dus de wisseling der jaargetijden te danken.
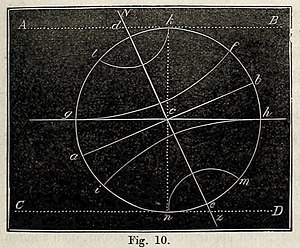
Stellen wij, dat de aarde op een zeker punt van hare baan gekomen, b.v. in fig. 1 in b, zoo geplaatst is, dat de Noordpool naar de zon, die wij hier als in het centrum c geplaatst vooronderstellen, is toegekeerd, dan zal het van de zon uitstralende licht in de rigting van de ecliptica tusschen de raaklijnen A B en C D op het ligchaam der aarde vallen, zooals in fig. 10 wordt voorgesteld. Wat zal dan het geval zijn? Het noordelijke halfrond heeft nu een veel grooter aandeel in het licht en de warmte der zon dan het zuidelijke: want terwijl de zon in het Noorden het deel des aardbols a c k beschijnt, en slechts k c b in de schaduw stelt, wordt daarentegen in het Zuiden slechts a c n beschenen, terwijl b c n in het duister ligt. In alle plaatsen boven den aequator gelegen, zullen dus de dagen langer dan de nachten zijn; beneden den aequator zal het tegengestelde plaats hebben. Hoe noordelijker men komt, des te langer zullen de dagen zijn, ja boven den Noordpool-cirkel l k is er in het geheel geen nacht meer, omdat dit geheele vlak zelfs bij de rondwenteling der aarde aan het zonnelicht is toegekeerd. Hoe zuidelijker men komt, des te langer zijn de nachten, en beneden den Zuidpool-cirkel wordt het in 't geheel geen dag meer. Het is zomer in het noordelijk en winter in het zuidelijk halfrond.—Stellen wij nu verder, dat de aarde na eenigen tijd in fig. 1 van b tot f is voortgegaan, dan valt in fig. 10 het licht vlak op haar. Het gevolg is dus, dat het noordelijk en zuidelijk halfrond gelijkelijk met licht en warmte bestraald worden, dat dus de dagen en nachten over de geheele aarde even lang zijn. Het is de tijd der nachtevening.—Is nu na eenigen tijd de zon [ 48 ]in fig. 1 in a aangekomen, dan zal juist het tegendeel plaats hebben van hetgeen wij zoo even zeiden. Het zonnelicht zal nu van de andere zijde tusschen de raaklijnen B D in fig. 10 op de aarde vallen. Het zuidelijk halfrond zal dus naar de zon zijn toegekeerd. Het zal zomer zijn in het Zuiden, terwijl in het Noorden de winter heerscht.—Gaat de aarde dan weder voort in hare baan tot g, dan zal er wederom een tijd van nachtevening op de aarde heerschen. Omdat de aarde met gelijkmatige snelheid op hare baan voortgaat, heeft ook de wisseling der jaargetijden met zachte overgangen plaats.
Was nu de aarde niet in dien schuinschen stand, maar b.v. regtstandig op hare baan gesteld, zoodat de aequator en ecliptica zamenvielen en de as der polen loodregt daarop stond, dan zouden het licht en de warmte der zon geheel gelijkmatig over de aarde verbreid zijn. Dag en nacht zouden overal even lang zijn. Alle afwisseling van jaargetijden zoude ophouden en de aarde eene eeuwige lente vieren.
Fig. 11 doet het ons duidelijk zien, dat van welke zijde de zon ook de aarde beschijnt, hetzij hare stralen van de zijde van A C of van de zijde van B D invallen, de verdeeling van licht en warmte overal onder alle breedten gelijk zal zijn.
Stellen wij ons daarentegen voor, dat de as der aarde geheel met hare loopbaan zamenviel, en dat bij gevolg haar aequator met [ 49 ]de ecliptica een' regten hoek maakte, dan zoude daaruit onvermijdelijk volgen, dat er, als de Noordpool naar de zon was gekeerd, op het noordelijk halfrond weken en maanden lang onafgebroken dag zoude heerschen, terwijl het van de zon afgekeerde zuidelijk halfrond in een even langen nacht zoude verkeeren.
Die schuinsche stand der aarde is echter niet onveranderlijk dezelfde. Als men de vroegste waarnemingen der sterrekundigen, waarvan die onder den Chineeschen keizer tschu-king 1100 v. C. wel de oudste zullen zijn, met de latere vergelijkt, dan vindt men, dat er eene langzame afneming van den schuinschen stand der ecliptica plaats heeft. Die jaarlijksche afneming wordt thans op ongeveer eene halve sekonde, of naauwkeurig uitgedrukt, 0", [ 50 ]berekend. Wanneer nu deze afneming geregeld voortging, dan zoude eenmaal de aequator en ecliptica zamenvallen, de hoek g c a en b c h op fig. 10 geheel verdwijnen en de in fig. 11 voorgestelde toestand werkelijk aanwezig zijn. Maar dit uitzigt op eene eeuwige lente, die dan zoude aanvangen, is geheel ongegrond. De juistere kennis van de wederkeerige aantrekking, die de verschillende ligchamen van ons planetenstelsel op elkander uitoefenen, heeft geleerd, dat dergelijke afwijkingen niet altijd in dezelfde rigting kunnen voortgaan, maar dat zij, tot een zeker punt gekomen, wederom in eene tegenovergestelde rigting overgaan. Het zijn, om zoo te spreken, langzame schommelingen, die wel eeuwen en duizenden jaren in ééne rigting voortgaan, maar dan ook weder even lang eene tegenovergestelde rigting volgen en zoowel in toenemen als in afnemen binnen bepaalde perken zijn ingesloten. Zoo heeft de sterrekundige lagrange berekend, dat de verandering in de schuinschheid van de ecliptica besloten is tusschen 21 en 28 graden. Het is dus eene slingering, die in duizentallen van jaren eenen boog van ongeveer 7 graden beschrijft.
De stelling der aarde op hare baan ondergaat nog eene aanmerkelijke verandering door de veranderde rigting van de as der aarde. Indien deze as onveranderlijk dezelfde rigting behield, dan zoude zij altijd op hetzelfde punt des hemels gerigt zijn. Een gevolg hiervan zoude zijn, dat de sterrenhemel met opzigt tot de aarde altijd in denzelfden stand zoude blijven. Dit is nu echter het geval niet. De ster, die nu wegens hare nabijheid aan de pool des hemels de poolster heet, is niet altijd poolster geweest en zal het niet altijd blijven.
Laat in fig. 13 de lijn a f de rigting van de as der aarde, die met eenen hoek van 66½° op hare baan a d b e staat, aanwijzen. Denken wij ons nu in het middelpunt van de vlakte der aardbaan eene loodlijnige as c k, die dus de as der ecliptica vormt. Nu zal de as der aarde niet altijd in de rigting a f blijven, maar zich langzamerhand omwenden. Gesteld, dat die as zich door de punten a l d b heen beweegt, dan zal zij, in b aangekomen, in eene geheel tegengestelde rigting b g geplaatst zijn. Gaat dan die om[ 51 ]wending der as voort door e, dan zal ze in a wederom tot den vroegeren stand zijn teruggekeerd. 
In dien zelfden tijd nu, waarin deze omdraaijing van de as der aarde plaats heeft, zal zij aan den hemel een cirkelboog f m i g h beschrijven, waarvan de as der ecliptica c k het middelpunt uitmaakt. Zij zal dus achtereenvolgend henen wijzen op die punten van den hemel, die in dien cirkelboog gelegen zijn. Maar door de veranderde rigting van de as der aarde, wordt ook haar aequator verplaatst en naar een ander gedeelte des hemels gerigt. De punten, waar de aequator door de ecliptica gesneden wordt, de zoogenoemde nachteveningspunten, zullen dus telkens op andere punten des hemels wijzen en de geheele ecliptica rondloopen.
Men denke echter niet, dat deze omdraaijing van de as der aarde in hare baan binnen een kort tijdsbestek volbragt wordt. De aarde wentelt zich in 24 uren om hare as. Zij volbrengt in 365 dagen 5 uren 48' 47" hare jaarlijksche reis om de zon. Maar de omwending van hare as wordt, zoo als door de naauwkeurige berekening van peters te Dorpat is gebleken, eerst volbragt in den tijd van 25700 jaren. De jaarlijksche verandering in de rigting van de as bedraagt derhalve slechts 50" of naauwkeurig uitgedrukt 50",2468. Men noemt dit den vooruitgang der nachteveningen of de praecessie der aequinoctiën.
Stellen wij nu eens, dat a f de tegenwoordige rigting van de as der aarde aanwijst, dan zal na ruim 3000 jaren de as in de rigting l m, na ruim 12000 jaren in de rigting b g geplaatst, en na 25700 jaren weder tot a f zijn teruggekeerd.
Hoe langzaam deze verandering nu ook plaats moge hebben, zoo is zij echter thans reeds duidelijk merkbaar. Door deze verandering toch worden de nachteveningspunten aan den hemel verplaatst. In [ 52 ]ruim 2000 jaren bedraagt die verplaatsing een twaalfde gedeelte van de ecliptica. Nu is men reeds sedert eeuwen gewoon de ecliptica in twaalf deelen af te scheiden, die naar zekere sterrebeelden worden genoemd b.v. de Weegschaal, de Maagd enz. Maar nu komen die deelen niet meer overeen met de sterrebeelden, waarnaar zij genoemd zijn, daar elk deel met opzigt tot het sterrebeeld, welks naam het draagt, één ten achteren is. Die afdeeling van den hemel, die men door het teeken van den Ram aanduidt, ligt niet in het sterrebeeld van den Ram, maar van de Visschen, en zoo vervolgens. Zeer natuurlijk: want sedert dien tijd, dat men voor ruim 2000 jaren elk deel des hemels naar het daarin zich bevindend sterrebeeld noemde, is de stand van de aarde met opzigt tot den hemel door de omwending van hare as, juist de lengte van een hemelteeken, dat is een twaalfde gedeelte van de ecliptica, verplaatst. Dit zal zoo voortgaan, tot, na verloop van omstreeks 25700 jaren, de afdeelingen des hemels weder volkomen zullen overeenstemmen met de sterrebeelden, wier namen zij dragen.
IV.
OVER DE BEWEGING DER AARDE IN HARE BAAN.
Het is allen bekend, dat de aarde zich op hare baan rondom de zon, al rondwentelende om hare as, voortbeweegt, dat zij die omwenteling in eenen tijd van 24 uren volbrengt, en dat zij ruim 365 zulke omwentelingen te volbrengen heeft, eer zij haren jaarlijkschen weg heeft afgelegd. Die beide bewegingen, om hare as en om de zon, zijn ten naauwste verbonden. Het is niet denkbaar, dat een ligchaam, van alle kanten vrij zijnde, zich alleen om hare as bewegen zal, zonder zich in de ruimte te verplaatsen. Wij kunnen de oorspronkelijke beweging der aarde ons niet anders denken, dan als een schok of stoot, haar reeds bij hare wording toegebragt. Geeft men eenen kogel, die op eene gladde vlakte ligt, eenen stoot, hij zal zich voorwaarts bewegen. Gaat die stoot juist door het middelpunt des kogels, hij zal in eene regte lijn voort[ 53 ]gaan, zonder dat er eene omdraaijing van dien kogel plaats heeft. Maar gaat die stoot niet juist door het middelpunt des kogels, dan zal hij zich tegelijk om zijne as wentelen, en die omwenteling zal met grootere snelheid plaats hebben, naarmate de stoot den kogel verder van het middelpunt treft. Zoo is het ook met onze aarde. Uit de omwenteling om hare as volgt reeds, dat zij zich ook in de ruimte moet voortbewegen uit kracht van de impulsie, die haar reeds bij hare wording is gegeven. Uit de snelheid van hare omwenteling heeft littrow (Wunder des Himmels, Appendix p. 33.) opgemaakt, dat die schok, die stoot, die oorspronkelijke impulsie aan de aarde moet zijn toegebragt op een punt 5 G.M. van haar middelpunt verwijderd.
Wij hebben boven reeds gezegd, dat de aarde op hare baan niet altijd met dezelfde snelheid voortgaat. De reden daarvan is gelegen in de gedaante van de baan, die de aarde doorloopt. Ware die baan volkomen cirkelvormig, dan zoude zij in elk punt des tijds met gelijke snelheid voortspoeden, omdat zoowel de kracht der aantrekking als die harer oorspronkelijke beweging, de centraal- en tangentiaal-krachten, in dit geval altijd gelijkmatig zouden werken.
Maar omdat de gedaante van de baan der aarde geene cirkelvormige, maar elliptische is, is ook de afstand tusschen de aarde en de zon niet altijd gelijk. Nu werkt de aantrekkingskracht in de omgekeerde rede der afstanden: dat wil zeggen, dat die kracht sterker is, naarmate de afstand der zich aantrekkende ligchamen geringer is en omgekeerd; en wel zoo, dat die kracht geëvenredigd is aan de vierkanten der afstanden. Wordt bij voorbeeld de afstand tusschen twee ligchamen tweemaal kleiner, dan zal de kracht van aantrekking tusschen die ligchamen tweemaaltwee, dat is viermaal grooter worden. Wordt de afstand driemaal verkleind, dan wordt de aantrekking driemaaldrie, dat is negenmaal vergroot. Daaruit volgt dus dat de kracht, waarmede de zon de aarde aantrekt, naar diezelfde evenredigheid grooter zal worden, naarmate de afstand kleiner is.
Als dus de aarde zich op het aan de zon naastgelegene punt, dat is, in haar perihelium, in b (zie fig. 1) bevindt, zal hare snel[ 54 ]heid de grootste zijn. Die snelheid zal van lieverlede afnemen, tot dat zij in haar aphelium, in a, gekomen is, om dan langzamerhand weder toe te nemen, totdat zij in haar perihelium hare grootste snelheid bereikt heeft.
Daar echter de ellips, die onze aarde rondom de zon beschrijft, slechts weinig van den volkomen cirkelvorm afwijkt, zoo kan ook het verschil tusschen hare grootste en kleinste snelheid niet zeer aanmerkelijk zijn. Als onze aarde het digtst bij de zon gekomen is en zij dus hare grootste snelheid bereikt heeft, legt zij in één uur 15100 G.M. af. Als zij het verst van de zon verwijderd is en dus hare kleinste snelheid heeft, gaat zij in één uur 14600 G.M. voorwaarts. Het verschil in de snelheid harer beweging bedraagt dus 500 G.M. in één uur.
Dat verschil in snelheid heeft ten gevolge, dat zij in gelijke tijdruimten, juist geene bogen van dezelfde lengte doorloopt. Aan den grooten en genialen kepler komt de hooge eere toe, dat hij de bewonderenswaardige natuurwet ontdekt heeft, volgens welke die verschillende grootheden worden bepaald.
Als men van de uiteinden van een' elliptischen boog voerstralen naar een der brandpunten trekt, dan besluiten twee dier voerstralen met eenen boog een driehoekig stuk, een zoogenaamden Sector. Zoo stellen op fig. 1 de vlakten k e b,i e k,h e i,a e h ons zulke sectoren voor. Heeft men nu twee bogen, die eene planeet in eene gelijke tijdruimte doorloopt, dan zullen niet die bogen even lang wezen, maar de vlakken, door die bogen en de voerstralen ingesloten, zullen even groot van inhoud zijn. Naarmate de planeet digter bij de zon geplaatst is, is dit stuk korter, maar moet het ook daarom breeder zijn, zal het dezelfde ruimte beslaan als een ander vlak, dat langer is, maar daarom ook smaller moet zijn. Vooronderstellen wij dat in fig. 1 de sectoren k e b,i e k,h e iena e h dezelfde ruimte bevatten, gelijken inhoud hebben, dan zal eene planeet de bogen b k,k i,i h,h a, die deze sectoren begrenzen, in dezelfde tijdruimte doorloopen. De snelheid zal dus in den boog b k aanmerkelijk sneller moeten zijn, dan in de volgende.
Men zoude zich echter zeer vergissen, indien men meende, dat [ 55 ]de aarde zich nu altijd juist in dat punt van hare baan bevond, en zich altijd juist met die mate van snelheid bewoog, zoo als dat volgens mathematische berekening zijn moest. Men moet niet denken, dat die baan, welke de aarde werkelijk om de zon beschrijft, eene volkomen elliptische lijn is, zoo als men die op mathematische gronden beschrijft en berekent. Dat zoude zeker het geval zijn, indien de zon het eenige ligchaam ware, tot hetwelk de aarde in betrekking staat. Maar er zijn nog andere ligchamen in ons planetenstelsel en daaronder van aanmerkelijke grootte, zooals de planeten Jupiter en Saturnus. En alle die ligchamen trekken elkander onderling aan, geheel volgens de zelfde wet, waarnaar de zon hare aantrekkingskracht uitoefent. Door die onderlinge aantrekking worden de planeten gedurig uit hare banen getrokken. Nu eens wordt hare beweging door de inwerking van eene andere planeet versneld, dan eens vertraagd. Men noemt deze afwijkingen gewoonlijk storingen.
Ook onze aarde ondergaat die storingen. Zij zijn van zeer verschillenden aard. Sommige hangen af van de tijdelijke standplaats, die deze of gene planeet ten haren opzigte inneemt en eene meerdere of mindere onregelmatigheid in hare beweging veroorzaakt. Omdat deze storingen in een bepaalden tijdkring wederkeeren, zoo noemt men ze periodieke storingen. Maar er zijn ook andere, die niet in de tijdelijke plaatsing der planeten, maar die in den bouw van het geheele planetenstelsel haren grond hebben en over reeksen van eeuwen loopen. Men noemt ze seculaire storingen.
Zoo ondergaat de vlakte, waarin de baan der aarde gelegen is, eene zeer langzame schommeling, die duizenden van jaren in eene rigting voortgaat, en dan weder duizenden van jaren in tegengestelde rigting terugkeert. De gedaante der baan zelve ondergaat eene kleine verandering, daar de groote as der loopbaan thans door lange tijdruimte henen inkrimpt, om zich later wederom uit te zetten.
Als wij alle deze storingen in aanmerking nemen, dan kunnen wij met regt beweren, dat onze aarde zich welligt nooit op dat punt van hare loopbaan bevindt, waarop zij zich volgens eenvoudige wiskundige berekening bevinden moest.
[ 56 ]Men denke echter niet, dat deze storingen uitzonderingen zijn op de wetten, die in de natuur zijn vastgesteld. Integendeel; ook die storingen worden te weeg gebragt door diezelfde kracht van aantrekking, die aan elk ligchaam naar evenredigheid van zijne massa eigen is.
Men denke evenmin, dat door die storingen eenig gevaar zoude kunnen ontstaan voor de orde en regelmaat, die in het geheele planetenstelsel heerschen. Men vreeze niet, dat daardoor ooit de gang van het geheel in verwarring zoude kunnen gebragt worden. De zon, die in massa onze aarde 360,000 en zelfs de grootste ons bekende planeet, Jupiter, nog 1000 malen overtreft, is onder de planeten, als een reus onder de dwergen. Zij is door hare ontzaggelijke massa de magtige gebiedster, die de beweging van alle van haar afhangende planeten bestuurt en regelt. Bovendien zijn de ligging en gedaante der loopbanen, de snelheid en omloopstijden der verschillende planeten, juist zoo geordend, dat, zoo als de hoogere wiskunde zulks ontegensprekelijk bewijst, elke afwijking, elke onregelmatigheid, elke storing telkens weder door zich zelve wordt hersteld, zoodat het geheele planetenstelsel in zijne oorspronkelijke door den Schepper zelven verordende inrigting den zekeren waarborg zijner duurzaamheid heeft. Het draagt niet, zoo als het werk van menschenhanden, de kiemen van zijne ontbinding in zich. Het kan en zal blijven bestaan, zoolang het Hem behaagt, die het eens te voorschijn riep en ordende.
V.
OVER DE VERPLAATSING VAN DIE BAAN IN DE RUIMTE.
Wij hebben tot hiertoe bij onze beschouwing van de baan der aarde de zon aangenomen als een vast en onbewegelijk punt in de scheppingsruimte, rondom hetwelk de aarde jaarlijks haren kringloop volbrengt. Maar de zon is niet zulk een vast en onbewegelijk punt: zij heeft zelve ook hare eigene beweging.
Het was reeds sedert langen tijd bekend, dat de zon zich even [ 57 ]als de aarde om hare as wentelt. Zij volbrengt die beweging in ruim 25 dagen. Maar nu is het reeds op zich zelven ondenkbaar, dat een ligchaam, hetwelk uit kracht van eene hem van den beginne af medegedeelde beweging, zich om zijne as wentelt, des niet te min onveranderlijk op dezelfde plaats zoude blijven. De omwenteling der zon om hare as sluit in zich, dat zij zich ook moet voortbewegen in de ruimte.
Deze gedachte werd het eerst duidelijk uitgesproken door bradley in 1748 en naderhand door de beroemdste sterrekundigen bevestigd. William herschell berekende reeds in 1783 uit eene menigte zeer naauwkeurige waarnemingen het punt aan den hemel, op hetwelk die beweging der zon gerigt is. Men scheen in het eerst de uitkomsten van herschell's onderzoekingen te betwijfelen. Maar argelander in 1837 en na hem lunddahl en struve zijn op het door herschell ingeslagen spoor voortgegaan en nagenoeg tot hetzelfde resultaat gekomen. Zij gingen echter nog eene schrede verder, en berekenden ook de snelheid waarmede de zon hare reis door de scheppingsruimte voortzet. Uit de laatste onderzoekingen van struve is gebleken, dat de zon zich voortbeweegt naar een punt des hemels, gelegen in het sterrebeeld van Hercules. Dit punt bevindt zich tusschen de sterren π en μ in het genoemde sterrebeeld, op 259°,4 R.O. en 33°,2 A.N. Zij doorloopt in die rigting jaarlijks eene ruimte van nagenoeg 30 millioenen G. M.
Onze zon behoort derhalve tot de vaste sterren en heeft even als deze eene eigene beweging. Alhoewel tot hiertoe alleen de rigting, welke de zon in die beweging volgt, met eenige zekerheid kan worden aangewezen, zoo moeten wij echter niet denken, dat zij zich in eene regte lijn voortbeweegt. Het lijdt wel geen twijfel, dat zij zich met het om haar zwevende planetenstelsel, misschien wel in vereeniging met eene geheele sterrengroep, rondom één gemeenschappelijk zwaartepunt in eene elliptische baan beweegt. Als de waarneming van den stand der zon, in betrekking tot de haar naastgelegene sterrengroepen zich over een aanmerkelijk gedeelte van hare baan zal uitstrekken, zal men eerst met wiskundige zekerheid het brandpunt kunnen aanwijzen van de verbazend groote ellips, [ 58 ]langs welke zij hare ontzaggelijke baan welligt in millioenen jaren volbrengt. De sterrekunde, die van de aarde tot het zonnestelsel en van het zonnestelsel tot het geheele sterren- en wereldstelsel opklimt, bestijgt daar eene hoogte, die de koenste verbeeldingskracht doet duizelen.
Uit de eigene beweging der zon om een of ander ver gelegen centraalpunt volgt van zelve, dat het geheele planetenstelsel en dus ook onze aarde, die er een lid van uitmaakt, haar op die onmetelijke baan vergezelt. Indien de zon in één jaar eene ruimte van 30 millioen G.M. doorloopt, dan wordt ook de geheele baan der aarde in dienzelfden tijd 30 millioen G. M. in de ruimte verplaatst.
Hoe aanmerkelijk deze verplaatsing ook zijn moge, zoo heeft zij echter niet den minsten invloed op de berekening van de loopbaan der aarde. Men kan daarbij de zon als een vaststaand en rustend punt beschouwen en hare beweging geheel buiten de berekening laten.
Maar geheel anders is het, als men vraagt naar den weg, dien onze aarde met der daad in de onbegrensde ruimte aflegt, als men de lijn, die zij door het onmetelijke ruim des heelals beschrijft, wil volgen. Wij nemen aan, dat de groote as van de baan der aarde, in ronde getallen uitgedrukt, 40 millioen G.M. lang is, en dat de zon in eene nagenoeg regte lijn 30 millioen G.M. in één jaar aflegt, dan zal de weg, dien onze aarde werkelijk in de ruimte doorloopt, eigenlijk eene spiraalvormig kromme lijn C D zijn, die op eene vlakte geteekend, nagenoeg de gedaante heeft, die wij in fig. 14 hebben afgebeeld. Elke afdeeling op de regte lijn A B stelt eenen afstand voor van 10 millioen G.M.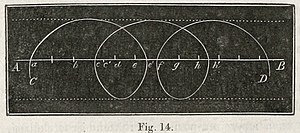
Stellen wij, dat de aarde zich op een zeker tijdstip in a bevindt, dan zal de zon in b zijn. Indien de zon zich niet voortbewoog, zou de aarde na een half[ 59 ]jaar in d zijn; maar omdat de zon zich in dien tijd 15 millioen G.M. verplaatst heeft, en zich dus in c' bevindt, zoo zal de aarde 20 millioen G.M. verder en dus in e' zijn. In het tweede halfjaar verplaatst de zon zich wederom 15 millioen G. M. en is dus van c' tot e voortgegaan; de aarde zal dus na verloop van dat halfjaar de lijn snijden op een punt, 20 millioen G.M. van e verwijderd, dat is in c. Zij zal van daar na een halfjaar tot h' en na een geheel jaar tot f zijn voortgegaan en zoo vervolgens.
Daar de aarde, als eene onafscheidelijke gezellin, de zon op haren weg door de oneindige ruimte getrouw moet ter zijde blijven, zoo volgt daaruit, dat zij ook nooit weder kan terugkeeren tot hetzelfde punt, hetwelk zij eenmaal heeft ingenomen. De plaats en de ruimte, waar wij ons op dit oogenblik bevinden, ligt reeds het volgende oogenblik vele mijlen achter ons. Terwijl wij met onze aarde in één jaar eene ruimte van 115 millioen G.M. doorklieven, ligt reeds het volgende jaar die geheele baan 30 millioen G.M. achter ons.
Zoo dringen wij, door onze aarde medegevoerd en gedragen, met eene verbazende snelheid de diepten der oneindige ruimte in. Hoe meer wij op dien weg voortgaan, des te meer zullen de geheimenissen des hemels zich voor den navorschenden blik der wetenschap ontsluijeren, des te dieper zal de harmonie des heelals door ons worden ingezien en begrepen.
Wat de sterrekunde op haar tegenwoordig standpunt reeds aan het licht bragt, is wel in staat ieders verbazing te wekken. Want zij heeft ons die ééne groote kracht doen kennen, die het gansche heelal, die myriaden werelden, talloos als het zand aan den oever der zee, in de onmetelijke scheppingsruimte langs hare vaste banen voortstuwt. En toch is het dezelfde kracht, die den waterdroppel vormt, den slinger beweegt, den opgeworpen steen weder ter aarde doet vallen, en die aan zonnestelsels en sterrengroepen hunne banen door alle tijdruimten henen heeft afgebakend. Eenvoudigheid van kracht en oneindigheid van werking! Is het niet het groote geheim des almagtigen Scheppers, hetwelk op elk gebied der natuur bij diepere nasporing zich telkens in klaarder [ 60 ]licht aan ons openbaart? Is het niet het beginsel, hetwelk de scheikundige telkens weder ontmoet, als hij het wonderbare zamenstel der dingen tot in hare grondbestanddeelen tracht te ontleden? Is het niet de regel, dien de kennis van het planten- en dierenrijk telkens weder aanwijst, als zij die eindelooze verscheidenheid in plant- en diervormingen, van de laagste trappen van het organische leven tot aan zijne hoogste ontwikkelingen volgt? Zet niet de geheele physiologie van den mensch, de diepere navorsching van zijn ligchaams- en geestesleven het zegel op dat groote scheppingsbeginsel, op dien regel, die geene uitzondering kent, die eeuwig onveranderlijk is, omdat zij haren grond heeft in den Almagtigen, die hemel en aarde heeft geschapen: Eenvoudigheid van kracht en oneindige verscheidenheid van werking!